Research

Research Interests

I blend mathematical theory from a range of fields including topology, geometry, combinatorics and algebra, to approach foundational questions about the behavior and properties of neural network functions. My thesis uses algebraic constructions from oriented matroid theory, geometric ideas from piecewise linear Morse theory, and fundamental constructions from algebraic topology. I write code, mostly in Python (Pytorch) and Sage, to obtain experimental and empirical measurements of the objects I study.

My background and research experiences additionally include applications of graph theory and topology in computational chemistry, materials science, and computer vision. I am interested in finding new applications of computational topology in the mathematical and natural sciences, and enjoy working on interdisciplinary projects.

Research

In Preparation (working titles)

• Combinatorial Regularity for Relatively Perfect Discrete Morse Gradient Vector Fields on ReLU Neural Networks. Robyn Brooks, Marissa Masden.

• A combinatorial approach to the separation capacity of “dendritic” classification functions. Caitlin Lienkaemper, Marissa Masden

Papers

• Automated Grain Boundary (GB) Segmentation and Microstructural Analysis in 347H Stainless Steel Using Deep Learning and Multimodal Microscopy. Shoieb Ahmed Chowdhury, M. F. N. Taufique, Jing Wang, Marissa Masden, Madison Wenzlick, Ram Devanathan, Alan L Schemer-Kohrn, Keerti S Kappagantula. Integrated Materials and Manufacturing Innovation, 2024.

Preprints

• Algorithmic Determination of the Combinatorial Structure of the Linear Regions of ReLU Neural Networks. 2022.

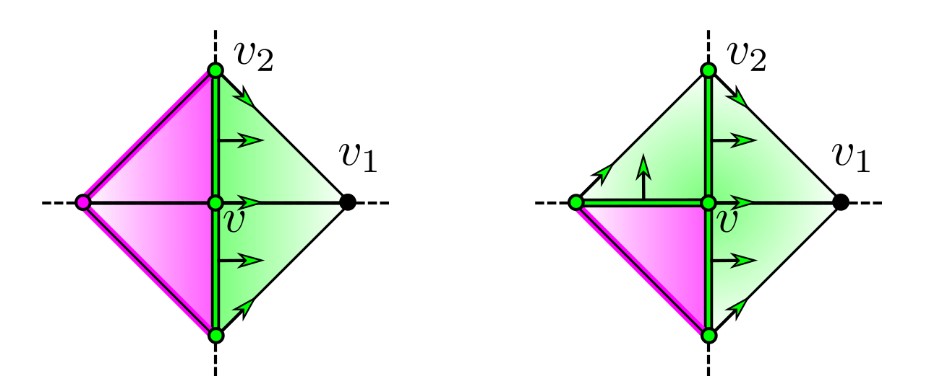
• Local and global topological complexity measures OF ReLU neural network functions. J. Elisenda Grigsby, Kathryn Lindsey and Marissa Masden, 2022.

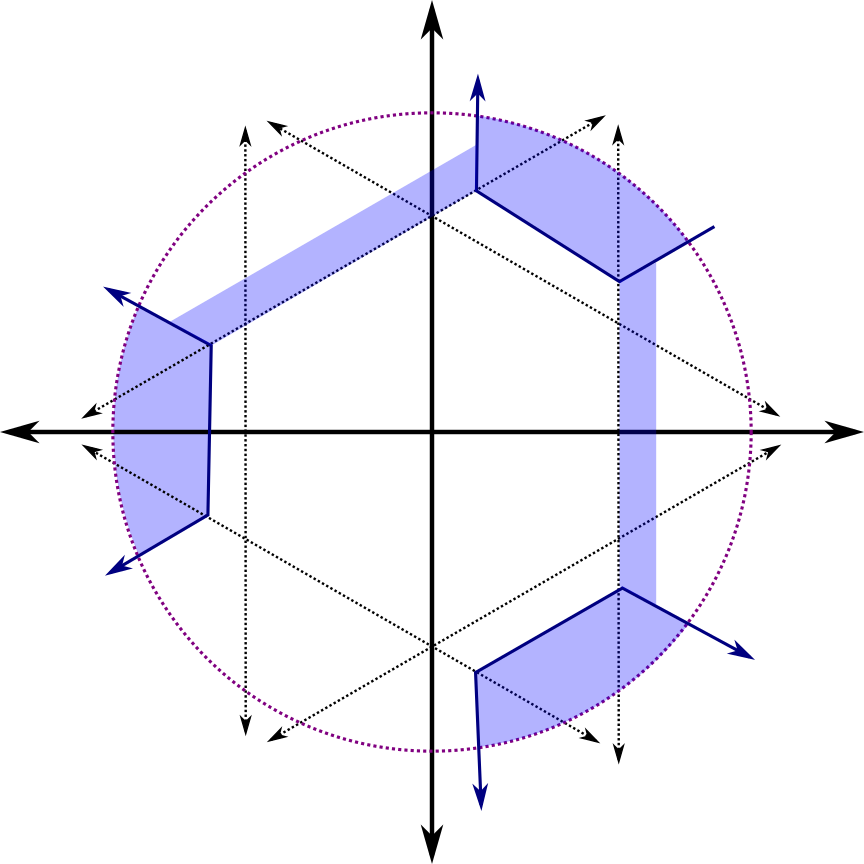
• Linear discriminant initialization for feed-forward neural networks. Marissa Masden and Dev Sinha, 2020.

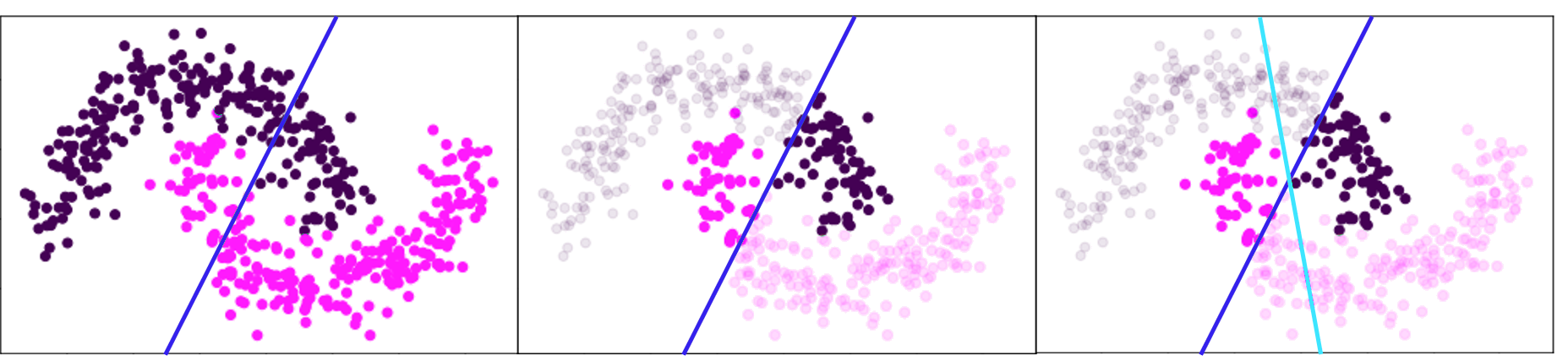
Other contributions

Alloy rupture strength prediction using machine learning and microstructure analysis. Ram Devanathan, Osman Mamun, Mohammad Taufique, William E. Frazier, Arun Sathanur, Keerti Kappagantula, Jing Wang, Marissa Masden, Madison Wenzlick, Kelly Rose. Advanced Characterization Techniques for Quantifying and Modeling Deformation, TMS 2023 Annual Meeting & Exhibition.

Contribution made during a graduate internship at Pacific Northwest National Labs through ORISE.

Understanding ReLU Activation Patterns through the Sign Sequence Cubical Complex. Poster at Applied Algebraic Topology Research Network Poster Session, October 8, 2021.

ChemNetworks 2.2 (polyhedra.c).

During an undergraduate internship at Washington State University, I implemented and iterated on a C algorithm (from an existing R algorithm) for detecting polyhedral structure in molecular dynamics simulations. This experience inspired my interest in computational geometry and topology.